This article was written by F. Habert and reviewed by B. d’Aligny and G. Morlat.
See the other articles we made on this theme !
Quantum cryptography was founded in the 1980s by Stephen Wiesner and showcases how we can better protect our communications by using quantum phenomena. Cryptography involves encoding messages or data in such a way that only authorized people can access and understand them. It is present in all the systems where information must securely travel, such as banking systems or internet communications. Unfortunately, quantum algorithms run on future quantum computers will be able to break most of our current cryptographic systems. Even if new classical algorithms could potentially be made more secure with Post Quantum Cryptography, there is still an urgent necessity for new types of encryptions. One approach is quantum cryptography, which leaverages quantum phenomena in order to protect our communications. A promising domain within quantum cryptography is Quantum Key Distribution (QKD), a method devised for securely sharing cryptographic keys between two parties, essential for subsequent classical encoding. This article aims to elucidate fundamental principles of both classical and quantum cryptography, illustrated with Quantum Key Distribution. We will also go through the status and barriers of implementing Quantum Key Distribution at scale.

Why cryptography, the threats of quantum computer attacks
Hackers are already storing significant amounts of encrypted data, anticipating future decryption via quantum computing. These attacks, known as “store now decrypt later”, are a real threat, as governmental information for example will still be valuable in the future decades. Moreover, with an always more interconnected world, cryptography will have a continuously more prominent role to play. We must find a way to encrypt our communications securely on the long term. But what does it mean to have a safe system of communication?
In a cryptographic system, we define unconditional security as a system which remains secure regardless of the computational capabilities of an adversary (i.e. a quantum computer or an extremely powerful classical computer), while computational security defines a system relying on the assumption that certain mathematical problems cannot be efficiently solved by a current machine. The latter definition forms the cornerstone of modern cryptography because the former has not been achievable yet. However, there is an increasing need to achieve unconditional security in our systems, given the potential of future computers. An example of a “computational security” made obsolete was Alan Turing’s device that successfully deciphered the German machine “Enigma”, utilized during WWII to encode the army’s positions.
Turing’s machine could perform significantly more computations than humans and was able to decrypt their messages.
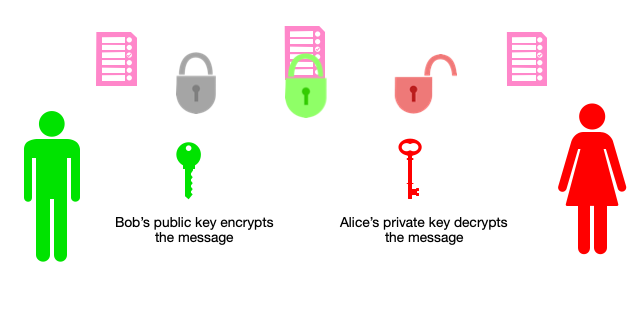
The computational security of our communications is currently based on the concept of “hard problems”, which are problems that a classical machine cannot break easily. The RSA algorithm for example is based on the fact that it is easy to compute the product of two very large prime numbers, but extremely hard to find them when given the resulting number! This is at the heart of public-private key encryption, securing how your credit card’s password travels on the internet during payments for example. The public key is freely distributable, allowing anyone to encrypt messages, but only the holder of the corresponding private key can decrypt them. Both are mathematically linked; the private key is derived from the factoring numbers of the public keys. Currently, safe public keys are based on 2048 bits, which means an actual number of 22048 possibilities, resulting in keys of 250 digits! For those types of public keys, a classical computer would take about 100,000 years to find the private key! This is the reason why cryptography is safe, as no entity possesses the computational power to break those algorithms in a reasonable amount of time. This is where quantum computing could play a game changing role


Shor’s algorithm
Shor’s algorithm is an algorithm that runs on a quantum computer, and hich would find the private keys from the public key in seconds. It was developed in 1994 by Peter Shor and undoubtedly pointed out the fragility of our cryptographic systems. Future eavesdroppers could possess quantum machines to run those quantum algorithms, making our system of communications at risk. This is where the “store now decrypt later” threat could become a reality. Therefore, cryptographic systems must urgently be reinforced by taking into consideration quantum superiority. There are currently two promising and complementary approaches to tackling this issue. Post Quantum Cryptography could render classical algorithms (i.e. RSA) less vulnerable by intensifying the underlying mathematics. New systems of cryptography based on quantum-like systems (i.e. Quantum Key Distribution) could also be implemented. In this article, we restrict ourselves to explaining of the latter.
Unconditional security : Quantum Key Distribution protocol
Quantum key distribution is a way to establish an unconditionally secure private key between two entities. This key can later be used for classical communications, to both encode and decode messages: we call this a symmetric key (in contrast to asymmetric keys like in the RSA protocol).
Quantum Key Distribution
Quantum Key Distribution consists in sharing a key by sending a quantum object to the correspondent. In this way, it utilizes the principle of quantum mechanics to guarantee that any eavesdropper would be noticed by the communicating parties. This therefore assures the two parties that they are the only one to be able to decode their respective messages.
No-cloning theorem
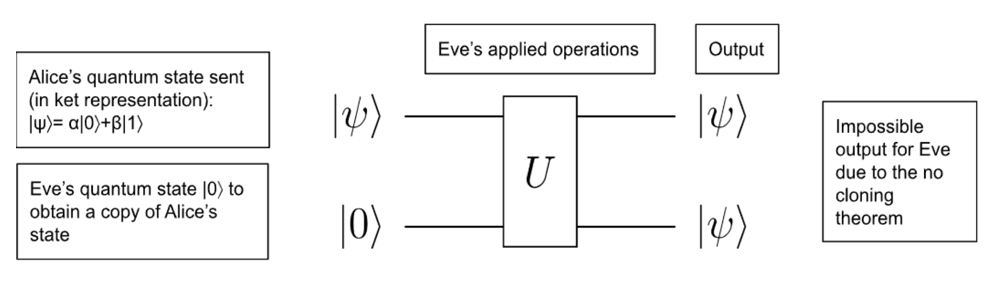
An important quantum physics principle that guarantees this is the fact that an eavesdropper cannot make a copy of the quantum information sent. If Alice is sending a quantum state to Bob, an eavesdropper, named Eve, will never be able to exactly copy the state without modifying it. This is known as the no-cloning theorem and it is a foundational level of security for the information being transmitted, as the distributed key cannot simply be intercepted and copied.
Measurement collapse
Furthermore, if Eve tries to measure the quantum state to obtain further information of it, she will collapse the state to its classical value, triggering Bob to detect the interference and flag the channel as compromised. This is referred to as the measurement collapse, preventing Eve from gaining knowledge over the system. Any other attempts made by Eve to manipulate the intercepted quantum state to extract additional information will inevitably introduce disturbances that will be detectable by the receiver. A quantum key distribution protocol, such as the B92 protocol, makes use of all those principles mentioned to establish a private key based on the measurement of those quantum states at the receiver’s side. In this protocol, the measurements outcomes of the quantum states are inherently unpredictable, making the key generation process non-deterministic. The key will be built gradually depending on Bob’s measurements.

Real life application of quantum key distribution
Quantum key distribution is currently being used in commercial, governmental, and financial sectors, but remains extremely dependent on the accuracy and good design of the physical system. It is mainly based on photons (i.e. a particle of light) in optical fibers, as they can travel fast and along great distances without interacting too much with their environment. They are polarized, which means that the photon will be aligned in a certain way. They can be for example in a horizontal or vertical orientation but as well in a mixture of those two. This polarization orientation is the quantum state used for sharing an encryption key.
Current obstacles to large scale adoption
There are still some barriers to creating scalable and widely used Quantum Key Distribution. First, the destruction of the photons occurs when it interacts with its environment: the longer the distance, the higher chances it gets destroyed. Quantum states of photons are extremely vulnerable to electromagnetic fields for example. The record for successfully running a QKD protocol stands at over 1.002 km along an optical fiber and was set by Chinese scientists from the University of Science and Technology of China. However, to mitigate environmental disturbances, the transmission is most efficient nowadays within smaller distances (i.e. 100 km). One way to ensure longer distances in QKD protocol is to use a quantum repeater which serves as logical connections designed to increase the range of QKD as it will maintain the coherence of the quantum.
The key rate is another important factor to consider for democratizing QKD, as it is the speed at which a key can be generated and exchanged between two entities.
Fast key generation would be essential in a commercial environment with large quantities of information to encode. However, the complex configurations of a widely used QKD network, and quantum repeaters could limit this speed. Finally, Quantum Key Distribution based on repeaters and optical fibers currently require costly and separate infrastructures. This will drastically impede the development of QKD.
For open-space links, a record distance of 1.200 km has already been accomplished for a satellite-to-ground QKD protocol by the University of Science and Technology of China. This could be immensely beneficial for creating secure communication channels between two countries, particularly when considering the limitations in terms of distances and cost associated with optical fibers. China has noticeably launched their first dedicated satellite for quantum communication, named Micius, which is orbiting at 500 km of altitude. It allows them to classically encrypt and decrypt data, using private keys set through quantum protocols. However, the key rate is way less than for optical fibers as a lot of photons are lost in the atmosphere during the process.
Conclusion
As we have seen, there is now a necessity to obtain safer ways of communication, and this can come from the creation of unconditionally secure private keys with quantum key distribution. It relies on proven quantum physical properties and is already being used commercially. However, many challenges remain ahead, such as the quality of the physical systems and the cost of the infrastructures. The limited key generation rate and transmission distance will also be important challenges to be overcome by QKD.
Our suggestions for curious readers
- Qutech Academy “How to secure communication”
- Qutech Academy “Quantum Key Distribution using BB84”
- Qutech Academy “Why making quantum repeaters is hard”
- Azuma, Koji, et al. “Quantum repeaters: From quantum networks to the quantum internet.”
- Mehic, Miralem, et al. “Quantum key distribution: a networking perspective.”
