This article was written by S. El Manouni and reviewed by B. d’Aligny and G. Morlat.
See the other articles we made on this theme !
Quantum computing is a field of computing that uses the principles of quantum mechanics to solve complex problems that our conventional computers will never be able to handle. These complex problems can be found in many fields, whether scientific, technological or industrial. This is particularly true for optimization problems in industries, where companies have to make heavy calculations in order to optimize their output, logistics and efficiency. Some of these calculations are impossible with current computers. Quantum computing could also have a real impact on the development of artificial intelligence, whose advances are constantly being observed, but which is still limited by the capacity of conventional computers. Indeed, the probabilistic calculations on which artificial intelligence is based could be greatly accelerated thanks to quantum algorithms. As a last example, in molecular chemistry, quantum computing could be useful for modelling molecular structures and interactions. This breakthrough could hold great promise for the development of new drugs, fertilizers, etc.
These problems take so much time to solve on a classical computer that they are simply considered unsolvable. Some of them would take over 13 billion years to solve with our most powerful supercomputers ! Quantum computing aims to solve them faster and more efficiently than conventional computers. The ultimate goal is to achieve what is known as “quantum supremacy”. This means that quantum computers could one day perform calculations that even the best classical computers could not, or at least not within a reasonable time.
A quantum computer could also be advantageous if it consumed less energy than a conventional computer to perform certain calculations. This concept is known as the “quantum energy advantage”.
As you can see, quantum computing will have a considerable impact on industry and research. In this article, we’ll look at the basic principles of quantum computing, its challenges and limitations, and briefly the different architectures of quantum computers.

Processing information on qubits
Before presenting the basic principles of quantum computing, it is essential to remind what a qubit is. The qubit is the quantum computer equivalent of the bit we manipulate on ordinary computers.
The bit (classical)
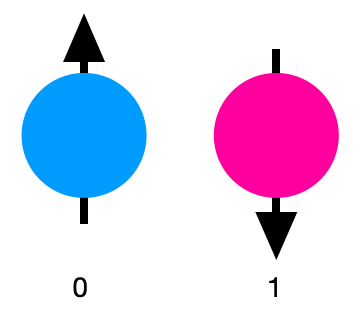
A bit is the smallest unit of information used by computers. It can be 0 or 1, and is used to program our computers when we assemble several of them on a circuit. It can be physically represented by an electric current. A classical circuit is made up of bits that pass through a set of logic gates such as NOT (which transforms a bit 0 into 1, and a bit 1 into 0), AND, or OR. These circuits are ultimately what makes computers perform all tasks such as browsing the internet, running programs, and performing calculations on devices like calculators.
The qubit (quantum)
Similarly, the qubit is the smallest unit of information used by quantum computers. But unlike the bit, the qubit can counter-intuitively be both 0 and 1 (noted |0> and |1>) at the same time. This is made possible by the superposition principle of quantum mechanics.
In practice, a qubit can be represented by certain characteristics of a quantum system – as the spin of an electron (a little arrow that represents how a particle is spinning around itself), the electronic level of an atom or the polarization of a photon (the direction in which light waves are vibrating) – which present properties of quantum mechanics (superposition, entanglement).
These qubits can be used for calculations in different ways. We will now introduce the two main quantum programming paradigms : gate-based quantum computing and analog quantum computing.
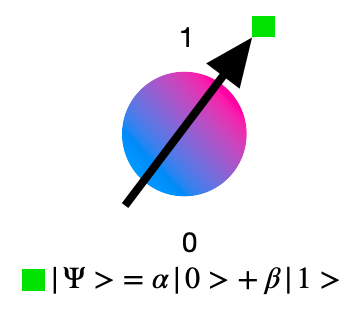
Gate-based quantum computing
Let’s start with gate-based computing. Gate-based or digital quantum computers manipulate qubits using quantum gates.
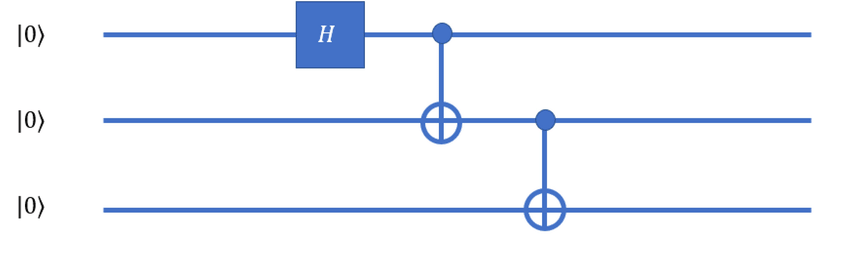
These quantum gates are equivalent to the logic gates NOT, AND, OR, NAND and NOR of our conventional computers. Here are a few examples of quantum gates.
X gate
One of the basic quantum gates is the X gate (or Not gate). This gate applies to a single qubit. The X gate transforms the qubit |0> into |1>, and vice versa |1> into |0>. When it is applied to the basis states |0> and |1>, the X gate has the same effect as the NOT gate on our ordinary computers. But it is more complex in general, as it acts differently when the qubit is in a superposition state.
Hadamard gate
A little more difficult to grasp, but just as important, is the Hadamard gate. If we consider a qubit |0> and this qubit passes through the Hadamard gate, it will find itself in a superposed state when it exits the gate. It will therefore be worth both |0> and |1> (written |0>+|1>). This gate can be understood as the “superposition” gate.
CNOT gate
There are also quantum gates that apply to two qubits at a time, in order to entangle them. This is the case with the CNOT gate. This gate takes two qubits as input and applies the X gate to the second qubit if the first is |1> . De facto, if the first qubit is worth |1> and the second is worth |0> (respectively |1>) then, after passing through the gate, the first qubit will always be worth |1> and the second will be worth |1> (respectively |0>). If the first qubit is worth |0>, both qubits remain unchanged. This gate can be understood as the “entanglement gate”.
Is gate based quantum computing useful yet?
We’re still a long way from seeing the first robust digital quantum computers for use in industry and research. Indeed, the physical qubits on which these computers are currently based still have too many errors. These errors are generated throughout the calculation process, when the qubits are manipulated, and are essentially due to quantum decoherence. Just a reminder, decoherence is due to interactions between qubits and their environment. It leads to the disappearance of the quantum properties of qubits, such as superposition. For instance, the qubits will end up being in the |0> or |1> state, but no longer a superposition of the two |0> + |1>.
NISQ
This limit in the development of digital quantum computers due to these errors defines what is known as the NISQ era, for Noisy Intermediate Scale Quantum. This term reflects the fact that today’s quantum computers have a limited number and quality of qubits, which make results very prone to decoherence errors. It does not mean that calculations are useless, but it gives us a limitation on the length and complexity of the achievable algorithms.
FTQC
In contrast, FTQC (Fault Tolerant Quantum computing) corresponds to quantum computing that will be delivered by computers containing a high number of qubits and a low error rate. This will only be achieved by correcting quantum errors. The first way to correct quantum errors is to use codes that enable them to do so, called quantum error correction codes (QEC). Several error-correcting codes have already been developed. These include stabilizing codes. This type of code enables errors to be detected and corrected without direct access to qubit information. There is also a way of reducing the impact of quantum errors without resorting to error-correcting codes : quantum error mitigation (QEM). This method relies on statistical calculations to attenuate the impact of quantum errors. An example is noise extrapolation, which involves performing the same quantum calculation several times with different levels of noise, in order to compare the results and extrapolate a noise-free result. Error correction can only work once the physical qubits have a good enough fidelity (low error rate). The first quantum error correction demonstrations were achieved recently, at the end of 2024.
Analog quantum computing
In contrast to digital quantum computers based on quantum gates, there are so-called analog quantum computers, which manipulate information in a continuous manner. They are based on continuous quantum systems. Analog quantum computing is mainly used to simulate quantum systems or solve optimization problems, and can work correctly with inferior quality qubits as for gate-based quantum computing. Unfortunately, it is also more restrictive than gate-based computing, as we cannot do any quantum algorithm using analog computing.
The difference between analog and digital quantum computers lies in the way they process information. Indeed, digital and analog are two methods of processing information. Digital represents information using discrete values (like the bits in our computers), whereas analog represents information using continuous variables, like signals, which are then reproduced and transmitted. Imagine the digital quantum computer as a set of well-organized, sequential steps, a bit like following a recipe with precise instructions.
Each step is like a specific instruction to be followed. On the other hand, the analog quantum computer works differently. Rather than following discrete steps, it can accomplish tasks with a single large step. It’s a bit like solving a problem in a single action, rather than following a series of steps.
Analog quantum computing is therefore the basis of quantum simulators. These can be used to simulate complex physical systems such as materials or molecules. The computation time required for these simulations on today’s supercomputers can be exponential, hence the interest here in using quantum computing.
For optimization problems, the analog quantum computing paradigm is the basis for quantum annealing. Quantum annealers are types of computer that allow certain optimization problems to be represented whose solution corresponds to the lowest energy level of a quantum system. This physical system gradually evolves from the highest energy state, representing a superposition of all possible solutions, to a lower energy state representing the optimal solution.

Quantum Emulation
Finally, in addition to quantum computers, some scientists are working on the development of quantum emulators. These are software programs run on conventional computers, notably supercomputers, that can execute quantum algorithms. Essentially, they enable quantum algorithms to be tested without using a quantum computer, based on very heavy calculations. However, they are severely limited by the storage capacity of the machines used, and can only emulate a certain number of qubits.
Quantum Computer Architecture
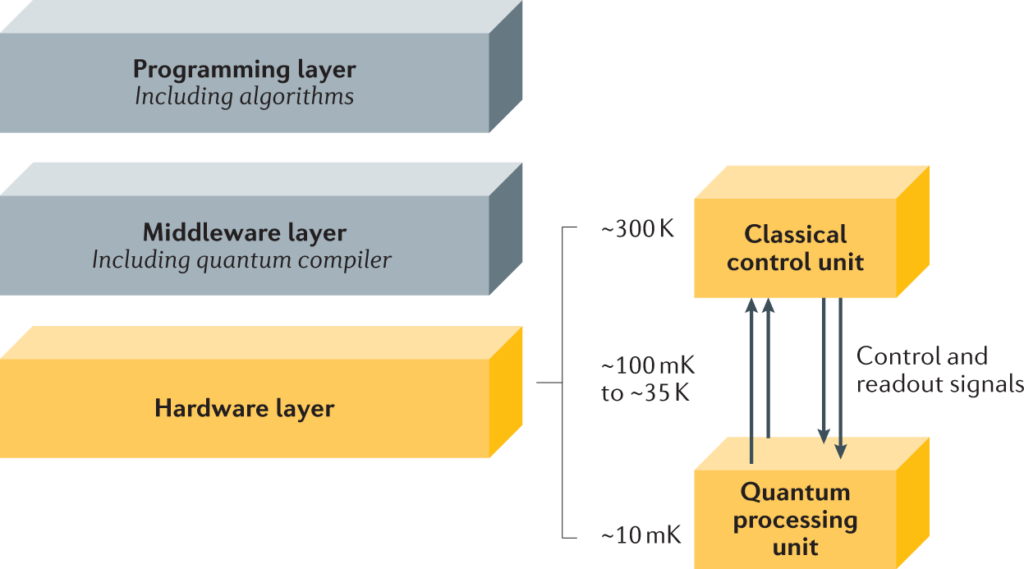
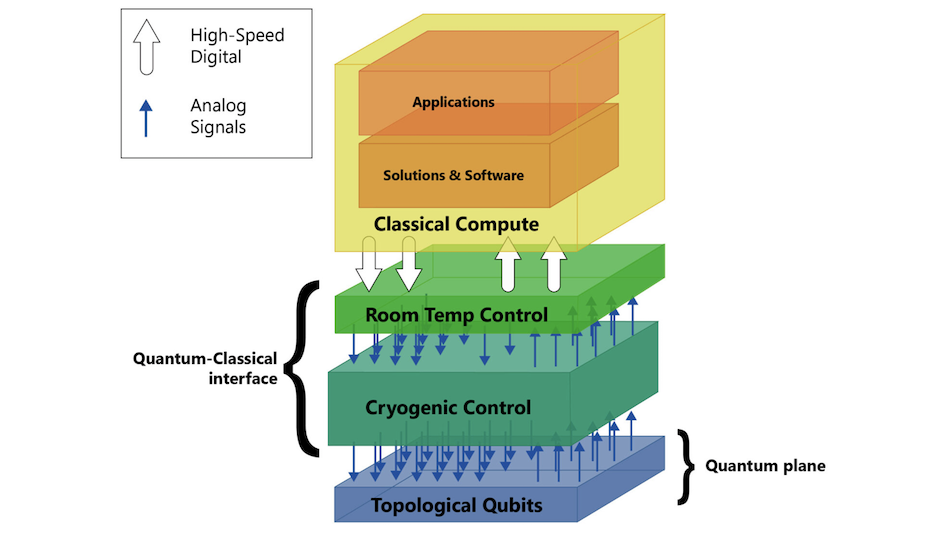
Quantum computer architectures are complex structures that represent the heart of quantum computing. Designing and building a quantum computer is a major challenge for physicists, engineers and researchers, both theoretically and practically.
There are different types of architecture, each presenting its own technical challenges and requiring specific expertise, reflecting the diversity and complexity of quantum computing. Their development requires considerable engineering effort to overcome the obstacles. A quantum computer requires 2 main parts : a control system and a quantum processing unit. The former is made of cables, classical electronics, or even lasers, to control the latter. A quantum processing unit is the part which is made of qubits, and conducts calculations. Both of these parts can be built in very various ways.
For instance, superconducting quantum computers rely on superconducting circuits to store and manipulate quantum information and are among the most mature platforms in quantum computing. Photonic quantum computers, on the other hand, exploit the unique properties of photons as a medium for quantum information. Photons are promising candidates for transporting and processing qubits because they do not interact too much with their environment: they are less prone to decoherence. However, for the same reasons of limited interaction strengths, it is difficult to apply gates on the qubits.
Conclusion
The advent of quantum computing promises to be a revolution that will radically transform many sectors. Thanks to its ability to process information exponentially more efficiently than conventional computers, quantum computing promises major advances in the optimization of industrial processes, the development of artificial intelligence, data security and healthcare. However, quantum computing faces major challenges such as quantum error correction and decoherence, which require ongoing innovation in technologies and theory. The different quantum computing paradigms, whether analog or gate-based quantum computing, face significant technical challenges in their development, although useful analog quantum computing is likely to emerge long before gate-based quantum computing. Finally, the different architectures of quantum computers, each with its specific advantages, are at the heart of current research aimed at turning this technological promise into reality.
Our suggestions for curious readers
- Le Lab Quantique article – Scaling a quantum computer to utility
- Qutech Academy “A framework for the future Quantum Computer
- Qutech Academy “How to build a qubit”
- Where are we heading with NISQ? Olivier Ezratty
- Keynote on superconduction qubits, Michel Devoret
- Henriet, Loïc, et al. « Quantum computing with neutral atoms. » (2020)
- Strohm, Thomas, et al. « Ion-Based Quantum Computing Hardware: Performance and End-User Perspective. » (2024)
- Wintersperger, Karen, et al. « Neutral atom quantum computing hardware: performance and end-user perspective. » (2023)
- Dalzell, Alexander M., et al. « Quantum algorithms: A survey of applications and end-to-end complexities. » (2023)
