Scaling quantum computers to utility ~ Le Lab Quantique

The biggest challenge for quantum computers to achieve practical computational power is scalability. This involves the ability to control many qubits while minimizing errors, allowing for the execution of complex algorithms. Significant advances for scalability are still required before quantum computers can have an impact in cryptography, finance, material science and machine learning routines.

To scale a quantum computer, several key characteristics must be optimized as much as possible, including qubit connectivity, coherence, gate time, and more. These characteristics vary depending on the hardware used (i.e. neutral atoms, trapped ions, photons and superconducting qubits). The primary challenge lies in enhancing these attributes while simultaneously increasing the number of qubits and extending algorithm runtimes.

In this article, we will explore the main concepts of scalability for digital based quantum computing but similar ideas may also apply to other approaches like analog quantum computing (for more information visit the introductory article 😉). We will highlight that there is no one-size-fits-all solution, but a variety of approaches are being used to get closer to a scalable quantum architecture !

Tatis Kontos and Lauriane Contamin, from the LPENS laboratory in Paris, working on the wiring of a dilution refrigerator (necessary to control quantum states). Photo by Hubert Raguet

Key performance indicators

To fully understand scalability, it’s essential to first grasp the key factors that influence the performance of a quantum processing unit (QPU).

Coherence time

It corresponds to the amount of time a qubit can maintain its quantum state before losing its quantum information. This can vary a lot between qubit technologies. For example, trapped-ion devices’ qubits have coherence times typically measured in seconds, whereas superconducting devices have coherence times in the range of microseconds (10−6 𝑠).

Gate fidelity

It ensures that the results obtained from a quantum circuit corresponds to the expected outcomes. It quantifies the closeness of the actual output state produced by the gate to the desired one, typically expressed as probability or percentage.

Gate speed

It tells us how fast a certain operation can be executed between qubits.

Connectivity

It refers to the number of qubits a given qubit can directly interact with. This indicator is very difficult to improve as it is deeply linked to the type of hardware one chooses.

Finding a balance

From these four concepts one can build performance indicators for comparing quantum processor architecture. In particular, the ratio of coherence time over gate speed tells us how many gates can be performed before the qubit loses its quantum information. Optimizing this ratio is therefore key to making quantum devices competitive.

More qubits, longer algorithms

Once these indicators are of good quality, the focus shifts to scaling up the number of qubits and the duration of the algorithms. However, as the number of qubits increases, so does the complexity of error management. Additionally, longer algorithms tend to introduce more noise into the system. This highlights the inherent difficulty of achieving scalability. Quantum processors designs have to consider the fact that they must keep their high performances with many qubits.

An in-depth look at connectivity

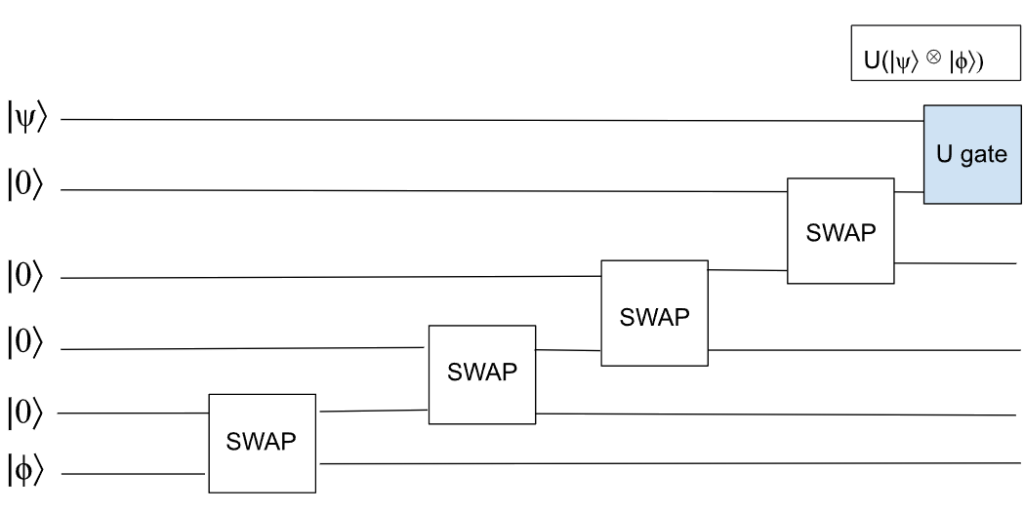
We need to add 4 SWAP gates in order to make |ϕ⟩ and |ψ⟩ interact in this nearest-neighbor connectivity situation

As previously mentioned, connectivity plays a crucial role in the performance of a quantum processor. For instance, certain qubit types, such as those used in trapped ion devices, offer what is known as “complete connectivity”, allowing any pair of qubits to be entangled regardless of their physical location.

Quantum processors based on neutral atoms also provide a high level of connectivity. In contrast, systems with nearest-neighbor connectivity, such as solid-state superconducting QPUs, face limitations on that matter.

Compensating finite connectivity

Systems with non-complete connectivity require additional operations to connect distant qubits, which can introduce more potential errors. For two physically distant qubits |ϕ⟩ and |ψ⟩ in a “nearest-neighbor connectivity”, SWAP gates (which swap two qubits’ states) are added to bring the state |ϕ⟩ closer to |ψ⟩, enabling the desired two-qubit gate to act on them. However, this comes at the cost of additional gates which increases the number of errors in the overall execution, and the algorithm’s total duration (see Figure).

Error accumulation

When designing a scalable quantum computer, it is key to understand that even a high-fidelity gate can perform poorly when used many times in a circuit. The probability of obtaining a correct result after operating 1000 gates of 99% fidelity is as low as 1%. Errors can even appear between gates, because qubits loose their coherence even when they are not being manipulated. We call this idle qubit fidelity. Gate and idle qubit fidelities change a lot between hardware approaches. Trapped ions qubits exhibit the highest gate fidelities (99.9% to 99.99%), and great idle qubit fidelities, while photonic quantum circuits have low-fidelity gates for two-photon quantum logic gates (CNOT or CZ). Indeed, complex mechanisms are required to make photons interact directly between each other and single photons still contain imperfections. Quantum engineers work to improve these KPIs with various techniques we will now introduce to you.

Improving the KPIs with better manufacturing and design

Improving the quality of manufacturing and design of the QPU is key for reaching KPI levels required for scalability. For example, advances in cryogenic systems (for superconducting and spin qubits) are essential to maintain the qubit’s coherence through minimum thermal noise (heat disturbing the qubits’ state). Improving superconducting materials from which superconducting qubits are made can also extend the coherence time. Other quantum computer technologies will require improvements in laser control (for neutral atoms and trapped ions quantum devices), integration of various optical components (for photonic qubits) and quantum control systems.

Concept view of Viqthor’s control system for cryogenic systems. Their goal is to use optical cables instead of electronic cables, to improve scalability and reduce the heat produced by the wires.

Changing the KPIs with new computing paradigms

Some hardware types have intrinsic flaws which limit the quality of some KPIs. But if one of the KPIs is too difficult to improve, why not change to a new one ? This is what has been done with measurement-based quantum computing (MBQC) – which is particularly promising for photonic quantum computers.

In MBQC, computation starts with a cluster state (a highly entangled state of multiple qubits), on which measurements and single qubit gates are performed to apply any gate on the remaining qubits. At each step, the measured qubits are lost for the rest of the calculation. In this configuration, the entanglement process is only needed at the begining and all further operations only reduce the number of qubits.

This approach is promising for photonic quantum computers, since it is easier to generate an initial (entangled) cluster state, than to implement two-photon gates along the road. But scaling photonic systems still requires to overcome challenges related to losses and precise measurements.

The necessity of error correction

As underlined previously, a quantum computer cannot scale without a robust design and manufacturing process. Yet perfect manufacturing is impossible, and errors will always occur. But luckily, software solutions can be used to compensate for the remaining errors on high quality quantum chips. We call this “error correction”.

For a better understanding of quantum error correction, let’s first describe its classical counterpart for classical computers. In the simplest classical error correction approach, we can “protect” our bit by using several bits to represent it through repetition code (i.e. 0 → 000). If an error occurs, such as a bit flip (i.e. 0 → 1), we can correct the error using “majority vote” (i.e. 001 → 1, 101 → 1). In this example, if the error rate is below the threshold of 1/3, errors will be corrected!

One difficult point is that we cannot directly apply classical error correction to our quantum processors. Indeed, the non-cloning theorem forbids us to duplicate a qubit’s state, meaning we can’t create multiple copies of the state |ψ⟩ as |ψ⟩|ψ⟩|ψ⟩ instead of just |ψ⟩. Additionally, we cannot directly measure the qubit in the middle of the calculation to correct it, as doing so would collapse its quantum state– thus destroying all the advantage of quantum computation. So, let’s see what an approach for quantum error correction could be.

Surface code

Distance 3 code – 17 physical qubit for 1 logical qubit (Google Quantum AI)

Distance 5 code – 49 physical qubits for 1 logical qubit (Google Quantum AI)

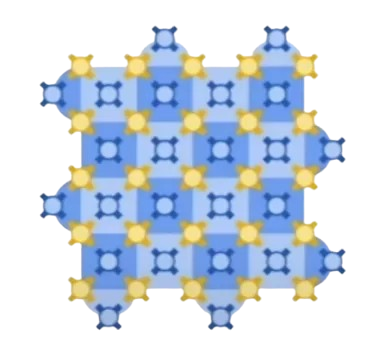
Surface code is an example of error correction that is implemented on a 2D grid of physical qubits. The idea is to encode logical qubits, abstracted error-protected qubits, onto many physical qubits. We can then apply measurements on some of those physical qubits, which will partially destroy the entanglement. But from the result we will be able to detect errors and apply gates to correct them. The entire 2D grid represents only a single logical qubit, and multiple such grids make up the QPU. The larger the grid for a single logical qubit, the more the information will be protected (with a certain threshold on the number of physical qubits that would eventually make the errors worse). It is a method with strong error tolerance, making it an efficient error correction technique. It is particularly used with superconducting qubits, making it a promising candidate for FTQC. Google and Amazon recently operated effective error correction for the first time, meaning they succeeded in reducing the amount of errors on the logical qubits, by increasing the size of the 2D physical qubit grids!

Scaling out

Welinq is a French startup which develops quantum memories, quantum links, and algorithms for distributed quantum computing and quantum networks

An interesting path for scaling quantum computers is to interconnect quantum processors to enhance the overall computational power. Managing errors on many QPUs can be easier than with one very large QPU. Distributed quantum computing may even allow different types of qubit-based devices to interoperate – thus taking advantage of each hardware’s strengths.

This would be possible by using photons to communicate between the QPUs and exchange information. Photons are indeed ideal for qubit transport as they can travel long distances and are very resistant to environmental noise. However, this will require to create quantum converters– machines which transfer the qubit’s information from one qubit type (neutral atom/ion/superconducting…) to a photonic state, and back. Scaling out would also require quantum memories to synchronize QPUs and make them operate in the right order. Despite these challenges, distributed quantum computing is another very promising way to increase the number of qubits, while overcoming the limitation of individual quantum processors!

Scalability takeaways

Fault-tolerant quantum computing (FTQC) refers to the era in which we will be able to perform any computation by employing efficient error correction techniques. Currently, the state of the art is represented by Noisy Intermediate-Scale Quantum (NISQ) devices, which are limited by inherent noise. This restricts the complexity of the circuits it can run, from the amount of information they can process (number of qubits) to the duration of the algorithms they can execute (number of gates). Therefore, scalability relies on quantum processors designed to perform computations reliably without errors and decoherence with an important number of qubits. To do so, we must improve manufacturing, chip design, and if necessary, change the way we apprehend quantum algorithms to find new quantum computing paradigms. Once we can run gates quickly on many qubits and with high quality, we can compensate for the remaining few errors with error correction and come closer to Fault Tolerant Quantum Computing!

Scaling quantum computers to utility